<그래프 용어>
- 정점 : (Node, Vertex)
- 간선(Edge) : 정점간의 관계를 나타낸다.
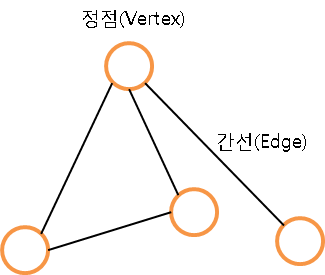
- 그래프 : 정점과 간선이 있는것
- 경로 : 간선의 연속(시작점 ~ 도착점 까지 정점을 거쳐 감)
- 최단경로 : 그래프의 경로 중 가장 짧은 것
- 사이클 : 경로인데, 시작점과 도착점이 같은 것
- 단순 경로/사이클 : 경로/사이클에서 같은 정점을 두 번 이상 방문하지 않는 경로/사이클
(특별한 말이 없으면, 일반적으로 사용하는 경로와 사이클은 단순 경로/사이클을 말한다.)
- 간선은 방향이 있을 수도 있고, 없을 수도 있다.
- 방향이 없는 그래프 : 양방향 그래프 (서로 오갈 수 있음)
- 방향이 없는 그래프는 저장을 할 수 없기 때문에 각 방향당 하나씩 총 두개 저장해 줘야 한다.
- 간선이 여러개일 수도 있다.
- 가중치 : 간선에 값이 들어있음 -> 비용과 관련
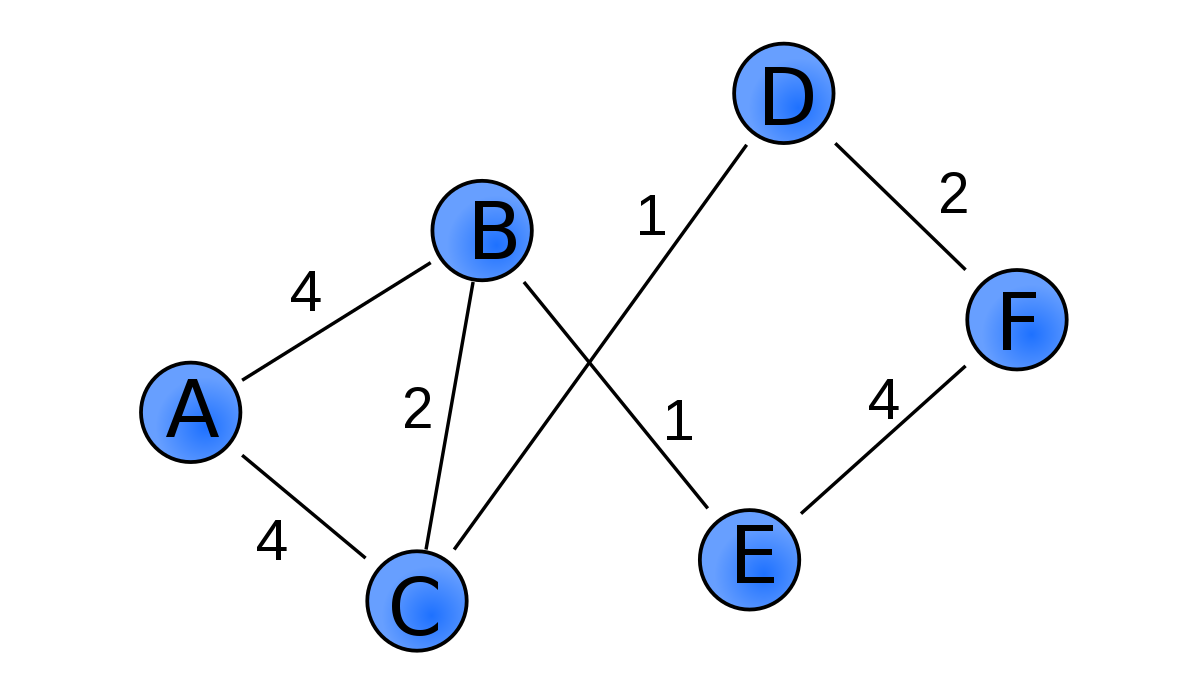
- 차수 : 정점과 연결되어있는 간선의 개수
<그래프 저장>
- 정점과 간선 둘 다 저장
- 정점 : 보통 갯수만 저장하면 됨
- 간선 : 다 저장해야함
=>결국 간선을 저장하는것을 의미하게됨, 어떤 정점 x와 연결된 간선을 효율적으로 찾기 위해 그래프 저장
<인접행렬>
2차원 배열의 그래프의 정보 저장
A[i][j] = 1 --> i에서 j로 가는 간선이 존재
A[i][j] = 0 --> i에서 j로 가는 간선이 존재하지 않음

<인접 리스트>
A[i] = i 와 연결된 정점(간선)과 그 간선의 가중치를 리스트로 저장하고 잇다.
인접리스트 저장시 동적배열 필요, 왜냐면 한 정점과 연결돼있는 선이 몇개가 될지 전혀 알 수 없어
링크드 리스트 사용(장점:크기를 동적으로 변경할 수 있다)

< 공간복잡도>
인접행렬 : O(V^2)
인접리스트 : O(E)
<인접행렬 vs 인접리스트>
1. 인접행렬
- 장점 1. 임의의 두 정점 u,v가 주어졌을 때, u -> v로 가는지 존재하는지 찾는데 O(1)만큼 걸림
- 장점 2. 두 정점 u,v가 주어졌을 때, v,u로 가는지 존재하는지 찾는것 또한 O(1) 만큼 걸림
2. 인접리스트
- u에 들어있는 간선을 다 찾아서 v가 존재하는지 찾는 방법 뿐 -> O(차수)
- A[v]에서 모든 간선 찾아야함
=> 어떤 간선이 존재하냐 or 그 간선의 역방향 간선이 존재하냐 이런경우에 인접행렬이 좋지만 공간이
너무 많이 필요 ㅇㅅㅇ -> 인접리스트 많이 사용
<간선리스트>
동적할당없이 인접리스트와 비슷한 효과를 냄
'알고리즘 > 알고리즘 개념' 카테고리의 다른 글
| 정렬 알고리즘 (0) | 2020.10.21 |
|---|---|
| 자료구조와 알고리즘 (0) | 2020.10.14 |
| 탐욕알고리즘(Greedy) (0) | 2020.08.22 |
| 다이나믹 프로그래밍 (0) | 2020.08.11 |
| 그래프의 탐색(DFS, BFS) (0) | 2020.08.04 |
